ぷよの手つなぎ実装
実現方法をわかっていれば、コード自体はすんなり思いつくようになって来た。
と言うわけで、ぷよの手つなぎ実装しまいた。
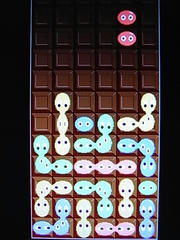
みごとにつながってます。
かわいいっ!(笑)
アルゴリズムで躓きまくったあとだから、思った事が一発で成功するとひときわ嬉しいね。
なんか、画面に動きが出た分、背景が真っ黒なのが気になってきた。
実行ファイル置いておきます。
ソースのテキストファイルも同じフォルダに入ってます。
http://u7.getuploader.com/game/download/69/%E3%81%B7%E3%82%88%E3%81%B7%E3%82%88%E5%86%8D%E7%8F%BE%E3%83%81%E3%83%A3%E3%83%AC%E3%83%B3%E3%82%B8%EF%BC%8316.zip
操作やダウンロードについては、#14あたりの記事を参照してください。
実現方法をわかっていれば、コード自体はすんなり思いつくようになって来た。
と言うわけで、ぷよの手つなぎ実装しまいた。
みごとにつながってます。
かわいいっ!(笑)
アルゴリズムで躓きまくったあとだから、思った事が一発で成功するとひときわ嬉しいね。
なんか、画面に動きが出た分、背景が真っ黒なのが気になってきた。
実行ファイル置いておきます。
ソースのテキストファイルも同じフォルダに入ってます。
http://u7.getuploader.com/game/download/69/%E3%81%B7%E3%82%88%E3%81%B7%E3%82%88%E5%86%8D%E7%8F%BE%E3%83%81%E3%83%A3%E3%83%AC%E3%83%B3%E3%82%B8%EF%BC%8316.zip
操作やダウンロードについては、#14あたりの記事を参照してください。
PR
ぷよの手つなぎについて考えてみる。
一応前回までで目標としていたゲーム性の本質の部分は再現できたと思うので、終わりにしようかとも思ったんだけど、ここまでやってくると色々追加したくなるわけで。
現時点で頭の中に次に作りたいものが明確にあればよいのだけど、今のところインベーダーみたいなスクロールのないシンプルなシューティングに挑戦してみようかなくらいのイメージしかない。
ある程度の完成イメージを持って作業に入らないとやばそうだってのは、今回のぷよぷよ再現で実感したので、次回作のイメージが固まるまでは惰性的にぷよぷよをいじってゆこうと思う。
どっちにしても演出や点数計算や表示、音楽、ゲームパッドのコンフィグなんかは避けて通れないと思うので、ぷよに対する愛着の続く限りやってみようかなと。
で、YOUTUBEなんかで動画をみたり、この間たまたま実物に触る機会があって(なんとメガドライブ版w)気になってはいたんだけど、つながったぷよは手をつなぐのよ。
手をつなぐってのは表現として適切かどうかわからんけども。
ようするに隣接したぷよ同士が絵的にもつながって引っ張り合ってるような感じになる。
「ああ、どうやって処理してるのかな」
と、うずいたわけです(笑)。
上下左右の4方向でつながる可能性があるから、ぷよの絵は単独の時のも含めて16パターン必要だなって直感的にわかった。
一瞬で脊髄反射のように16って数字が出てきたから自分でも驚いて、なんでかなと少し考えた。
どうやら、小学生時代に雑誌(たぶんBASICマガジンとか・・・知らないかw)で勉強した2進数を脳が覚えていたみたい。
当時、0と1だけで書いたキャラクターのドットパターンを16進数に変換してプログラムのデータに格納するってのをやってた記憶がボンヤリある。
ぷよの手つなぎの方向は4方向でそれぞれの方向の状態を1と0で表す。
1ならつないでる、0ならつないでないって感じで。
そうすると4桁の2進数が必要になる。
4桁の2進数は、ちょうど1桁の16進数で表せる。
この流れで僕の頭に「全部で16パターン」ってイメージが出てきたようだ。
子供の頃にやったことって、なんで20年以上やってなくても出てくるんだろう。
で、今の脳みそで考えてみた。
2進数で表せるってことは、上下左右を調べて状態ごとにフラグを立てて4つのフラグの状態を調べて絵を選んで表示するって流れが、かなり簡略化できる。
上を1桁目、左を2桁目、下を3桁目、右を4桁目で表現する。
それぞれつながっている時、
上 0001
左 0010
下 0100
右 1000
計 1111
て感じで全方向の状態が2進数の足し算で求められるのだ。
実際には10進数か16進数に変換して計算すると思うけど、グラフィックハンドルを入れておく配列変数に2進数の順番通りに絵を格納しておけば、計算結果を配列変数の [ ] の中に入れるだけで必要なてつなぎぷよの絵を表示することが出来るんじゃないか。

これは意外と簡単に実装できそうだ。
ゴールにたどり着く目処がたつと、がぜんモチベーションが上がる。
取り合えず各色16パターンの手つなぎぷよを描いて2進数の並びで並べたBMPファイルを作った。
絵自体はコピー&ペースト&回転・反転を駆使して、できるだけ楽した。ので、出来については触れないように!w

手抜きしたわりには、けっこう可愛く描けてるじゃん!
と、自分では思っていたりする。
誰も言ってくれないし。
一応前回までで目標としていたゲーム性の本質の部分は再現できたと思うので、終わりにしようかとも思ったんだけど、ここまでやってくると色々追加したくなるわけで。
現時点で頭の中に次に作りたいものが明確にあればよいのだけど、今のところインベーダーみたいなスクロールのないシンプルなシューティングに挑戦してみようかなくらいのイメージしかない。
ある程度の完成イメージを持って作業に入らないとやばそうだってのは、今回のぷよぷよ再現で実感したので、次回作のイメージが固まるまでは惰性的にぷよぷよをいじってゆこうと思う。
どっちにしても演出や点数計算や表示、音楽、ゲームパッドのコンフィグなんかは避けて通れないと思うので、ぷよに対する愛着の続く限りやってみようかなと。
で、YOUTUBEなんかで動画をみたり、この間たまたま実物に触る機会があって(なんとメガドライブ版w)気になってはいたんだけど、つながったぷよは手をつなぐのよ。
手をつなぐってのは表現として適切かどうかわからんけども。
ようするに隣接したぷよ同士が絵的にもつながって引っ張り合ってるような感じになる。
「ああ、どうやって処理してるのかな」
と、うずいたわけです(笑)。
上下左右の4方向でつながる可能性があるから、ぷよの絵は単独の時のも含めて16パターン必要だなって直感的にわかった。
一瞬で脊髄反射のように16って数字が出てきたから自分でも驚いて、なんでかなと少し考えた。
どうやら、小学生時代に雑誌(たぶんBASICマガジンとか・・・知らないかw)で勉強した2進数を脳が覚えていたみたい。
当時、0と1だけで書いたキャラクターのドットパターンを16進数に変換してプログラムのデータに格納するってのをやってた記憶がボンヤリある。
ぷよの手つなぎの方向は4方向でそれぞれの方向の状態を1と0で表す。
1ならつないでる、0ならつないでないって感じで。
そうすると4桁の2進数が必要になる。
4桁の2進数は、ちょうど1桁の16進数で表せる。
この流れで僕の頭に「全部で16パターン」ってイメージが出てきたようだ。
子供の頃にやったことって、なんで20年以上やってなくても出てくるんだろう。
で、今の脳みそで考えてみた。
2進数で表せるってことは、上下左右を調べて状態ごとにフラグを立てて4つのフラグの状態を調べて絵を選んで表示するって流れが、かなり簡略化できる。
上を1桁目、左を2桁目、下を3桁目、右を4桁目で表現する。
それぞれつながっている時、
上 0001
左 0010
下 0100
右 1000
計 1111
て感じで全方向の状態が2進数の足し算で求められるのだ。
実際には10進数か16進数に変換して計算すると思うけど、グラフィックハンドルを入れておく配列変数に2進数の順番通りに絵を格納しておけば、計算結果を配列変数の [ ] の中に入れるだけで必要なてつなぎぷよの絵を表示することが出来るんじゃないか。
これは意外と簡単に実装できそうだ。
ゴールにたどり着く目処がたつと、がぜんモチベーションが上がる。
取り合えず各色16パターンの手つなぎぷよを描いて2進数の並びで並べたBMPファイルを作った。
絵自体はコピー&ペースト&回転・反転を駆使して、できるだけ楽した。ので、出来については触れないように!w
手抜きしたわりには、けっこう可愛く描けてるじゃん!
と、自分では思っていたりする。
誰も言ってくれないし。
できる限り急ぎ足でやってきた。
必要な知識はそのつど調べて勉強しながら。
家族持ちなので1日にPCに向かって作業できる時間はいいとこ2時間くらいだ。
それでも、夢中になりやすい性格なので、仕事の休憩時間とかちょっと出来た時間があれば、すぐにノートを出して要素を書き出して検討してみたり、どんなプログラムコードで実現できるか考えてみたりしていた。
大好きなビールもかなりひかえた。
晩酌は習慣なんだけど、なにせ酒が入ると頭が回らなくなる上に記憶が怪しくなるのだ(笑)。
プログラミングのために酒を絶つ男・・・。
妻はね・・・あきれてる(笑)。
一銭の金にもならんし、35にもなって今さらソフトウェア開発者になれるわけでもないだろう。
僕もそんなことはわかっている。
うちにMZ-2200があって、BASIC遊びに夢中になっていた小学生のころ、プログラマーやゲームクリエーターを夢見たことがあった。
そのころ抱いていた未来の自分のビジョンを最近鮮明に思い出した。
そのビジョンはあんまり輝いていて、小学生のころの自分に申し訳なくなった。
ネットが普及し、コンピューターの性能が飛躍的に高くなった現在を、小学生のころの僕が見たらどう思うだろう。
開発環境は無料で提供され、必要な知識はネット上にいくらでも転がっている。
「お前なにやってんだよ!」
小学生の自分にそう言われた気がした。
「あれも、これも、できるじゃん!」
わかってるよ。
でも、もう僕は大人になってしまったんだよ。
お前みたいに無限の可能性も、時間も無いんだよ。
でも、一方でもう1つの考えが頭をよぎった。
テトリスを再現しようとして挫折したあの頃より、僕はたくさんの経験を積んできた。
いろんな事も考えた。
いろんな事にチャレンジしてきた。
基礎的な事を応用してより高度なものを構築する力もジャンルは違えどたくさんの仕事で学んできた。
もうあまりにも時間がたって忘れてしまったから、コンピューターの知識やプログラミングの技術に関しては、小学生や中学生のころの僕の方が上かもしれない。
それでも、脳みそは今の僕の方が上だ。
それだけは断言できる。
小学生のころの僕には将来、「あんなふうになりたいなあ。」とか、「あんな事が出来るようになりたいなあ。」って事がいっぱい、いっぱいあった。
そのいっぱい、いっぱいあった事のひとつくらい、(たとえプロじゃなくたって)出来る大人になってあげてもいいんじゃないかな。
そう思った。
それだけのことなんだ。
必要な知識はそのつど調べて勉強しながら。
家族持ちなので1日にPCに向かって作業できる時間はいいとこ2時間くらいだ。
それでも、夢中になりやすい性格なので、仕事の休憩時間とかちょっと出来た時間があれば、すぐにノートを出して要素を書き出して検討してみたり、どんなプログラムコードで実現できるか考えてみたりしていた。
大好きなビールもかなりひかえた。
晩酌は習慣なんだけど、なにせ酒が入ると頭が回らなくなる上に記憶が怪しくなるのだ(笑)。
プログラミングのために酒を絶つ男・・・。
妻はね・・・あきれてる(笑)。
一銭の金にもならんし、35にもなって今さらソフトウェア開発者になれるわけでもないだろう。
僕もそんなことはわかっている。
うちにMZ-2200があって、BASIC遊びに夢中になっていた小学生のころ、プログラマーやゲームクリエーターを夢見たことがあった。
そのころ抱いていた未来の自分のビジョンを最近鮮明に思い出した。
そのビジョンはあんまり輝いていて、小学生のころの自分に申し訳なくなった。
ネットが普及し、コンピューターの性能が飛躍的に高くなった現在を、小学生のころの僕が見たらどう思うだろう。
開発環境は無料で提供され、必要な知識はネット上にいくらでも転がっている。
「お前なにやってんだよ!」
小学生の自分にそう言われた気がした。
「あれも、これも、できるじゃん!」
わかってるよ。
でも、もう僕は大人になってしまったんだよ。
お前みたいに無限の可能性も、時間も無いんだよ。
でも、一方でもう1つの考えが頭をよぎった。
テトリスを再現しようとして挫折したあの頃より、僕はたくさんの経験を積んできた。
いろんな事も考えた。
いろんな事にチャレンジしてきた。
基礎的な事を応用してより高度なものを構築する力もジャンルは違えどたくさんの仕事で学んできた。
もうあまりにも時間がたって忘れてしまったから、コンピューターの知識やプログラミングの技術に関しては、小学生や中学生のころの僕の方が上かもしれない。
それでも、脳みそは今の僕の方が上だ。
それだけは断言できる。
小学生のころの僕には将来、「あんなふうになりたいなあ。」とか、「あんな事が出来るようになりたいなあ。」って事がいっぱい、いっぱいあった。
そのいっぱい、いっぱいあった事のひとつくらい、(たとえプロじゃなくたって)出来る大人になってあげてもいいんじゃないかな。
そう思った。
それだけのことなんだ。
まだまだ検索アルゴリズムの話
いや、1週間くらいでゲーム性の再現は出来るんじゃないかと思ってたんだけど、甘くないね。
消えるブロックの検索アルゴリズムはテトリスよりかなり高度なんじゃないかと。
今ならテトリスは挫折せずに再現できる気がする・・・。
で、検索アルゴリズムについて前回に引き続き。
このアルゴリズムは、上り下りの回数さえ適切なら、どんな形の並びでもきちんとグループ分け出来る。
ただし、その回数が問題だった。
前回、登り、下り、登りの3回で行けるみたいなこと書いたんだけど、ぜんぜん足りない(笑)
だいたい、フィールドの横幅しか考えてない時点で終ってる。
アルゴリズムが正しくても、使い方が間違っていた。
自分の頭の悪さにがっかりしたよ。
で、横6ブロック、縦13ブロックで考えられるもっとも(アルゴリズムにとって)過酷な並びを考えてみた。
このアルゴリズムは、登り検索は右下方向に強く、左方向には1ブロックしか追えず、上方向にいたっては最弱で1ブロックも追う事が出来ない。
下り検索はその逆だ。
これは検索の流れを前回の記事で確認してもらえばわかると思う。
で、ことごとく検索方向を潰す最悪な並びを紙に書いて、完全に検索し終わるまで何往復必要か計算してみた。
その結果、8往復・・・。
もちろん実際にゲーム中にフィールドのブロックを全て使ってそんな並びで消す状況なんかありえないんだけど、これまでの制作の流れから過信は禁物と思い8往復を実装した(笑)。
いや、今のPCの性能は素晴らしいね。
その程度のループじゃ体感速度はまったく変らない。
僕が小学校のころBASICで遊んでたMZ-2200と比較したらいったい何倍くらいの速さなんだろう(汗)。
今のPCだってPEN3の1Ghzくらいだったはずだから、ぜんぜん現役スペックじゃないんだけどね。
と言うわけで、アルゴリズムの出来としてはいまいちかも知れんけど実用十分てことで許してください。
とは、言ったものの、頭の中に他の方法(アルゴリズム)も浮かんでいるので、我慢できなくなったら試してみます。
最後に今回のアルゴリズムについて前回の記事で漏れがあった部分を補足説明しときます。
group.Member[ グループナンバー ] と言う配列変数を定義して、各グループのメンバー数(つながったぷよの数)を管理しています。
インデックスの段階では通し番号なので当然この配列変数には全て1が入っています。
その後、登り下りの検索のなかでグループの結合が起こるたびに、group.Member[ 生き残ったグループ番号 ] が+1、group.Member[ 吸収されたグループ番号 ] が-1となります。
検索が終了すると、group.Member を参照して、メンバー数が4以上になったグループを洗い出し、フィールド配列を検索してそのグループ番号が入っている座標を消します。
あとは出来た隙間の上に浮いているぷよを落下させて、新しい配列でまたインデックスからやり直します。
連鎖がおき続ける限り、この処理を繰り返すわけです。
このアルゴリズムは恐らくぷよぷよを再現する方法の中で最もと言っていいほど、シンプルで幼稚で効率の悪いアルゴリズムだと思います。
(しかも本当に完全かどうか自信もない・・・)
それでも作り始めた時点で、僕の頭にはこれの原型となるアイデア(前の方の記事で失敗に終ったやつ)しか無く、初心者が開発環境をインストールして2週間やそこらで作れるのはこの辺がいいとこかと・・・。
でも、それだけに、ここを読んでいる方に僕のような初心者の方がいるなら、わりと理解しやすいアルゴリズムだったんじゃないかとも思います。
現在は他の方法もぼんやり頭の中にあります。
それは検索ロボット型アルゴリズムと名づけたい感じのもので、つながったぷよを法則に従ってグループ結合しながらわたり歩き、最初の検索座標につながっている数を持って帰ってくるというものです。
イメージが伝わりにくいですかね、すいません(笑)。
これはこれで、はたして上手く行くのか試してみたい気持ちがあるので、そのうち作ってみるかもしれません。
では、実行ファイルを。
8往復(笑)検索バージョンです。
見た目上は何も進化してなくてすいません。
http://u7.getuploader.com/game/download/66/%E3%81%B7%E3%82%88%E3%81%B7%E3%82%88%E5%86%8D%E7%8F%BE%E3%83%81%E3%83%A3%E3%83%AC%E3%83%B3%E3%82%B8%EF%BC%8315.zip
変更箇所は検索部分のループだけなので、変更のあった検索関数のみソースのテキストファイルを同梱しています。
ダウンロード、実行に当たっての手順は#14の記事などを参照してください。
いや、1週間くらいでゲーム性の再現は出来るんじゃないかと思ってたんだけど、甘くないね。
消えるブロックの検索アルゴリズムはテトリスよりかなり高度なんじゃないかと。
今ならテトリスは挫折せずに再現できる気がする・・・。
で、検索アルゴリズムについて前回に引き続き。
このアルゴリズムは、上り下りの回数さえ適切なら、どんな形の並びでもきちんとグループ分け出来る。
ただし、その回数が問題だった。
前回、登り、下り、登りの3回で行けるみたいなこと書いたんだけど、ぜんぜん足りない(笑)
だいたい、フィールドの横幅しか考えてない時点で終ってる。
アルゴリズムが正しくても、使い方が間違っていた。
自分の頭の悪さにがっかりしたよ。
で、横6ブロック、縦13ブロックで考えられるもっとも(アルゴリズムにとって)過酷な並びを考えてみた。
このアルゴリズムは、登り検索は右下方向に強く、左方向には1ブロックしか追えず、上方向にいたっては最弱で1ブロックも追う事が出来ない。
下り検索はその逆だ。
これは検索の流れを前回の記事で確認してもらえばわかると思う。
で、ことごとく検索方向を潰す最悪な並びを紙に書いて、完全に検索し終わるまで何往復必要か計算してみた。
その結果、8往復・・・。
もちろん実際にゲーム中にフィールドのブロックを全て使ってそんな並びで消す状況なんかありえないんだけど、これまでの制作の流れから過信は禁物と思い8往復を実装した(笑)。
いや、今のPCの性能は素晴らしいね。
その程度のループじゃ体感速度はまったく変らない。
僕が小学校のころBASICで遊んでたMZ-2200と比較したらいったい何倍くらいの速さなんだろう(汗)。
今のPCだってPEN3の1Ghzくらいだったはずだから、ぜんぜん現役スペックじゃないんだけどね。
と言うわけで、アルゴリズムの出来としてはいまいちかも知れんけど実用十分てことで許してください。
とは、言ったものの、頭の中に他の方法(アルゴリズム)も浮かんでいるので、我慢できなくなったら試してみます。
最後に今回のアルゴリズムについて前回の記事で漏れがあった部分を補足説明しときます。
group.Member[ グループナンバー ] と言う配列変数を定義して、各グループのメンバー数(つながったぷよの数)を管理しています。
インデックスの段階では通し番号なので当然この配列変数には全て1が入っています。
その後、登り下りの検索のなかでグループの結合が起こるたびに、group.Member[ 生き残ったグループ番号 ] が+1、group.Member[ 吸収されたグループ番号 ] が-1となります。
検索が終了すると、group.Member を参照して、メンバー数が4以上になったグループを洗い出し、フィールド配列を検索してそのグループ番号が入っている座標を消します。
あとは出来た隙間の上に浮いているぷよを落下させて、新しい配列でまたインデックスからやり直します。
連鎖がおき続ける限り、この処理を繰り返すわけです。
このアルゴリズムは恐らくぷよぷよを再現する方法の中で最もと言っていいほど、シンプルで幼稚で効率の悪いアルゴリズムだと思います。
(しかも本当に完全かどうか自信もない・・・)
それでも作り始めた時点で、僕の頭にはこれの原型となるアイデア(前の方の記事で失敗に終ったやつ)しか無く、初心者が開発環境をインストールして2週間やそこらで作れるのはこの辺がいいとこかと・・・。
でも、それだけに、ここを読んでいる方に僕のような初心者の方がいるなら、わりと理解しやすいアルゴリズムだったんじゃないかとも思います。
現在は他の方法もぼんやり頭の中にあります。
それは検索ロボット型アルゴリズムと名づけたい感じのもので、つながったぷよを法則に従ってグループ結合しながらわたり歩き、最初の検索座標につながっている数を持って帰ってくるというものです。
イメージが伝わりにくいですかね、すいません(笑)。
これはこれで、はたして上手く行くのか試してみたい気持ちがあるので、そのうち作ってみるかもしれません。
では、実行ファイルを。
8往復(笑)検索バージョンです。
見た目上は何も進化してなくてすいません。
http://u7.getuploader.com/game/download/66/%E3%81%B7%E3%82%88%E3%81%B7%E3%82%88%E5%86%8D%E7%8F%BE%E3%83%81%E3%83%A3%E3%83%AC%E3%83%B3%E3%82%B8%EF%BC%8315.zip
変更箇所は検索部分のループだけなので、変更のあった検索関数のみソースのテキストファイルを同梱しています。
ダウンロード、実行に当たっての手順は#14の記事などを参照してください。
今度こそ検索アルゴリズム出来たんじゃない?
前回の記事で『完成!』とか言っといて、非常に恥ずかしいのだけど、普通に穴がありました。
今度こそ大丈夫だと思います。
ではアルゴリズムの流れを。
前回のは忘れてください(笑)
~インデックス~
フィールドのぷよ全てに上段・左優先で通し番号をつけます。
これは必ず最初に1回行う処理で、この番号がそのままつながったぷよのグループ番号になります。
~登り検索~
配列内を下の図の順番でブロックごとに検索します。
①→→→→→→
②→→→→→→
③→→→→→→
④→→→→→→
~以下略~
各ブロックごとの検索は以下のように行います。
①右となりのブロックが自分と違う番号で、かつ同じ色ならば、小さい方の番号で結合する。
②下のブロックが自分と違う番号で同じ色ならば、自分の番号で結合する。
~下り検索~
配列内を下の図の順番でブロックごとに検索します。
~以上略~
←←←←←←④
←←←←←←③
←←←←←←②
←←←←←←①
各ブロックごとの検索は以下のように行います。
①左となりのブロックが自分と違う番号で、かつ同じ色ならば、小さい方の番号で結合する。
②上のブロックが自分と違う番号で同じ色ならば、自分の番号で結合する。
登り検索も下り検索も、検索の進行方向と逆に伸びる枝には1ブロック分しか追いつけないので、検索の進行方向と逆方向に2ブロック以上の長さで枝分かれするぷよのつながりは追いきれない。
これは、つまり片道分の検索が対応できるのはフィールドの横幅2ブロック分までだということを意味してるんじゃないだろうか。
実際2ブロック幅ならどんな形にぷよが並んでも、登り検索1回でグループ分けが完了する。
ところが3ブロック幅だと、例えばコの字につながった場合などで登り検索だけでは対応できなくなる。
111
001
511
こんな感じで、上の図の5の部分が検索からもれてしまうのだ。
この問題は下り検索を加えることで解決できる。
しかし、今度は4ブロック幅までは問題ないのだけど、5ブロック幅になると検索からもれるケースが出てくる。
00000
00000
10112
11102
例えば上の図の2の部分がそれだ。
これに対応するためには、もう一度登り検索を行わなければならない。
つまり、このアルゴリズムはフィールドの横幅が2ブロック増えるごとに、登り検索と下り検索を交互に追加して対応するアルゴリズムと言える。
ぷよぷよのフィールドは横幅が6ブロックなので、登り下り登りと3回検索する必要があるのだ。
もしも、8ブロック幅のぷよぷよを作りたいなら、更に1回下り検索を追加すれば対応できるはずだ。
いやー、こんだけ解説してまた穴があったら立ち直れないかも・・・。
実行ファイル置いておきます。
フォルダ内にソースコードのテキストファイルも入っています。
http://u7.getuploader.com/game/download/60/%E3%81%B7%E3%82%88%E3%81%B7%E3%82%88%E5%86%8D%E7%8F%BE%E3%83%81%E3%83%A3%E3%83%AC%E3%83%B3%E3%82%B8%EF%BC%8314.zip
上のリンク先、下のほうの「同意します」をクリックでダウンロードできます。
ポップアップブロックされる場合はウィンドウ上の情報バーをクリックして「ファイルダウンロード」を選んでください。
zipファイルなので、解凍してからフォルダ内のexeファイルをダブルクリックで実行されます。
操作方法は前回(#13)の記事を参照してください。
4つ以上つながったのに消えない!って言うようなバグを発見した場合は、消えなかったつながり方をコメントで報告いただけると助かります。
僕の方もデバッグしながら、今後の方針を考えたいと思います。
前回の記事で『完成!』とか言っといて、非常に恥ずかしいのだけど、普通に穴がありました。
今度こそ大丈夫だと思います。
ではアルゴリズムの流れを。
前回のは忘れてください(笑)
~インデックス~
フィールドのぷよ全てに上段・左優先で通し番号をつけます。
これは必ず最初に1回行う処理で、この番号がそのままつながったぷよのグループ番号になります。
~登り検索~
配列内を下の図の順番でブロックごとに検索します。
①→→→→→→
②→→→→→→
③→→→→→→
④→→→→→→
~以下略~
各ブロックごとの検索は以下のように行います。
①右となりのブロックが自分と違う番号で、かつ同じ色ならば、小さい方の番号で結合する。
②下のブロックが自分と違う番号で同じ色ならば、自分の番号で結合する。
~下り検索~
配列内を下の図の順番でブロックごとに検索します。
~以上略~
←←←←←←④
←←←←←←③
←←←←←←②
←←←←←←①
各ブロックごとの検索は以下のように行います。
①左となりのブロックが自分と違う番号で、かつ同じ色ならば、小さい方の番号で結合する。
②上のブロックが自分と違う番号で同じ色ならば、自分の番号で結合する。
登り検索も下り検索も、検索の進行方向と逆に伸びる枝には1ブロック分しか追いつけないので、検索の進行方向と逆方向に2ブロック以上の長さで枝分かれするぷよのつながりは追いきれない。
これは、つまり片道分の検索が対応できるのはフィールドの横幅2ブロック分までだということを意味してるんじゃないだろうか。
実際2ブロック幅ならどんな形にぷよが並んでも、登り検索1回でグループ分けが完了する。
ところが3ブロック幅だと、例えばコの字につながった場合などで登り検索だけでは対応できなくなる。
111
001
511
こんな感じで、上の図の5の部分が検索からもれてしまうのだ。
この問題は下り検索を加えることで解決できる。
しかし、今度は4ブロック幅までは問題ないのだけど、5ブロック幅になると検索からもれるケースが出てくる。
00000
00000
10112
11102
例えば上の図の2の部分がそれだ。
これに対応するためには、もう一度登り検索を行わなければならない。
つまり、このアルゴリズムはフィールドの横幅が2ブロック増えるごとに、登り検索と下り検索を交互に追加して対応するアルゴリズムと言える。
ぷよぷよのフィールドは横幅が6ブロックなので、登り下り登りと3回検索する必要があるのだ。
もしも、8ブロック幅のぷよぷよを作りたいなら、更に1回下り検索を追加すれば対応できるはずだ。
いやー、こんだけ解説してまた穴があったら立ち直れないかも・・・。
実行ファイル置いておきます。
フォルダ内にソースコードのテキストファイルも入っています。
http://u7.getuploader.com/game/download/60/%E3%81%B7%E3%82%88%E3%81%B7%E3%82%88%E5%86%8D%E7%8F%BE%E3%83%81%E3%83%A3%E3%83%AC%E3%83%B3%E3%82%B8%EF%BC%8314.zip
上のリンク先、下のほうの「同意します」をクリックでダウンロードできます。
ポップアップブロックされる場合はウィンドウ上の情報バーをクリックして「ファイルダウンロード」を選んでください。
zipファイルなので、解凍してからフォルダ内のexeファイルをダブルクリックで実行されます。
操作方法は前回(#13)の記事を参照してください。
4つ以上つながったのに消えない!って言うようなバグを発見した場合は、消えなかったつながり方をコメントで報告いただけると助かります。
僕の方もデバッグしながら、今後の方針を考えたいと思います。
- ABOUT
やってやれないことはないっ!たぶん・・・
- カレンダー
| 12 | 2026/01 | 02 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 最新コメント
[11/09 CALL MY NAME]
[11/09 erin]
[08/18 うずランド]
[07/11 うずランド]
[06/23 うずランド]
- プロフィール
HN:
Call my name
年齢:
51
性別:
男性
誕生日:
1974/05/22
職業:
スロ屋店員
趣味:
いろいろ
自己紹介:
やる気だけはあるつもりです。
はい。
はい。
- ブログ内検索
- カウンター
- アクセス解析

